en de
12. Veröffentlichung des ADµP® Entwicklernetzwerkes
Bitte wählen Sie in der Kopfzeile eine Sprachversion, eine der nachfolgenden Internet-Verknüpfungen oder Überschriften aus dem Inhaltsverzeichnis aus!
(«) Erste Veröffentlichung (<) Vorhergehende Veröffentlichung (>) Nachfolgende Veröffentlichung (») Letzte Veröffentlichung (^) Autor (=) Redaktion ($) Bestellung des ausführlichen Textes (&) Liste der Veröffentlichungen (§) Liste der Firmenschriften
Art der Veröffentlichung:
Vortrag zum Workshop Physik und Informatik am 15./16. März 1999 in Heidelberg (Auszug)
Thema:
Codieren zeitlicher oder räumlicher Verläufe physikalischer Schwingungen und Wellen in die Zahlendarstellung (Width of Step Coder/Decoder)
Autor:
Christian E. Jacob
Inhaltsverzeichnis: (0) Zusammenfassung  (1) Einführung  (2) Vereinbarung zum Funktionsraum  (3) Auflösung der Haupteinheiten  (4) Codierung  (5) Decodierung  (6) Anwendungen  (7) Literaturverzeichnis 
topic   (0) Zusammenfassung
Der Vortrag bezieht sich auf [Jacob 98]. Dort wird ein Verfahren zum Codieren zeitlicher oder räumlicher Verläufe in die Zahlendarstellung und Decodieren aus der Zahlendarstellung beschrieben. Zielstellung der Codierung und Decodierung ist die effiziente Weiterverarbeitung der unverfälschten Verläufe durch Mikrocontroller, Digitale Signalprozessoren, jede andere geeignete Hardware in Abhängigkeit von Informationsgehalt, sowie die audiovisuelle Darstellung. Maßnahmen der Signalvorverarbeitung und Datenkomprimierung entfallen. Der Anteil der analogen Verarbeitung wird minimal. U. a. werden dadurch systematische Fehler bei der Kodierung vermieden. Das beschriebene Verfahren wird einerseits in Algorithmen überführt (Programmbibliothek), die in Software- oder Firmware-Lösungen u.a. zum Komprimieren von Daten, dem Ermitteln von Kennwerten, der Analyse und audiovisuellen Darstellung verwendet werden. Andererseits wird aus der Verfahrensbeschreibung direkt das Layout von Hardware-Lösungen (Baugruppen, Schaltkreise, IP-Cores) generiert, die u.a. für die automatische Sprach- und Bildverarbeitung, die Subanalyse oder Merkmalsbildung verwendet werden.
topic   (1) Einführung
Nachteile der herkömmlichen Analog-Digital-Umsetzung sind hinlänglich bekannt: Mit Quantisierungsfehlern muss gerechnet werden. In Abhängigkeit von der Qualität des Antialysing-Filters enthält die digitale Darstellung mehr oder weniger übertastete Anteile. Eine etwaige Abtast-Halte-Schaltung verursacht zusätzliche Fehler. Eine Weiterverarbeitung der digitalen Darstellung mit einer Diskreten Fourier-Transformation z. B. der FFT ist hin und wieder problematisch. Auch Produkt- (Auto- und Kreuzkorrelationen) oder Phasendarstellungen entsprechen oft nicht der notwendigen Genauigkeit. Sollen die Fehler, die durch ein Abtasten entstehen, verringert werden, erhöht sich der technische Aufwand für das Abtastverfahren beträchtlich.
Anstelle der herkömmlichen Abtastung wird ein Verfahren zum Codieren der zeitlichen oder räumlichen Verläufe physikalischer Größen in die Zahlendarstellung vorgeschlagen, bei der die erreichbare Genauigkeit und der technische Aufwand in vernünftiger Relation zueinander stehen. Das Verfahren wird so beschrieben, dass es einerseits in Algorithmen für Software- oder Firmware-Lösungen (Programmbibliothek) umgesetzt werden kann. Andererseits kann es aber auch für Hardware-Lösungen in ein Layout überführt werden.
Anwendungen werden beim Erfassen, Übertragen und Auswerten physikalischer Größen in den Bereichen Multimedia, Mess-, Diagnose-, Automatisierungstechnik und Strukturanalyse gesehen. In dieser Anwendungsbreite ist das Verfahren sowohl für Physiker und Mathematiker als auch Informatiker und Techniker von Interesse. Die gewählte Darstellungsweise spricht Einsteiger genauso wie den versierten Informatiker, der auf dem Gebiet der Signalanalyse tätig ist, an.
topic   (2) Vereinbarung zum Funktionsraum
Für die mathematische Beschreibung des Verfahrens wird ein Funktionsraum vereinbart. Er hat (m + 1) Dimensionen, die wiederum durch eine Anzahl von (m + 1) Einheitsvektoren vu0, vu1, ..., vuµ, ..., vum vorgeben werden. Die Bezeichner der Dimensionen
µ, m Î N (Gl. 2.1)
sind Elemente der Natürlichen Zahlen.
Der Einheitsvektor vu0 wird als Basisvektor bezeichnet. Seine Richtung stimmt mit einer (nebenläufigen) Zeitachse, der Bewegungsrichtung einer (sich kreisförmig) ausbreitenden Welle oder der Scann-Richtung eines Bildes überein. Alle anderen Einheitsvektoren vu1, vu2, ..., vuµ, ..., vum stehen orthogonal zum Basisvektor vu0. Die Länge aller Einheitsvektoren ist definitionsgemäß
|vu0| = |vu1| = , ..., = |vuµ| = , ..., = |vum| = 1 (Gl. 2.2)
und wird in der Schreibweise u0, u1, ..., uµ, ..., um als Haupteinheit der jeweiligen Dimension verwendet.
Der µ-te Einheitsvektor vuµ repräsentiert also die µ-te Dimension im Funktionsraum mit der Haupteinheit uµ. Die der die µ-te Dimension zugeordnete Einheitsfläche auµ ergibt sich zu
auµ = uµ*u0 (Gl. 2.3)
Die Position eines Punktes An im Funktionsraum wird durch einen Vektor van charakterisiert. Er entsteht durch die Addition der jeweils mit der skalaren Größe aµ bzw. a0 verlängerten Einheitsvektoren vuµ und vu0:
van = aµ*vuµ +a0*vu0 (Gl. 2.4)
Die Länge des Vektors va beträgt:
_____________
|van| = an = Ö aµ2 + a02 (Gl. 2.5)
Der zeitliche oder räumliche Verlauf einer physikalischen Größe kann durch eine ausgewählte Punktefolge An im Funktionsraum wiedergeben werden. Die Punktefolge An wird dann bezogen auf Gl. 2.4 durch ausgewählte Wertepaare des Verlaufes An(aµ, a0) mathematisch beschrieben.
Die Position eines weiteren Punktes B in der Ebene, die von den Einheitsvektoren vuµ und vu0 aufgespannt wird, wird durch den Vektor
vb = bµ*vuµ + b0*vu0 (Gl. 2.6)
charakterisiert. Die Länge des Vektors vb beträgt:
______________
|vb| = b = Ö bµ2 + b02 (Gl. 2.7)
Der zeitliche oder räumliche Verlauf einer physikalischen Größe kann auch durch eine kontinuierliche Punktefolge B, die eine unendlich dichte Anordnung von Punkten enthält, im Funktionsraum dargestellt werden. Die Punktefolge B wird dann bezogen auf Gl. 2.6 durch den kontinuierlichen Verlauf bµ(b0) beschrieben.
Der Abstand zwischen den Punkten An und B wird durch den Vektor vc, der vom Punkt An nach Punkt B gerichtet ist, beschrieben:
vc = vb - van = cµ*vuµ + c0*vu0 (Gl. 2.8)
Weil die Einheitsvektoren vu0 und vuµ orthogonal zu einander stehen und die Punkte An und B in einer Ebene liegen, können die Größen cµ bzw. c0 aus den skalaren Größen, die in den Gl.n 2.4 und 2.6 eingeführt wurden, gewonnen werden:
c0 = b0 - a0 (Gl. 2.9)
cµ = bµ - aµ (Gl. 2.10)
Die Größen cµ und c0 entsprechen kontinuierlichen Katheten eines rechtwinkligen Dreiecks mit der kontinuierlichen Fläche:
acµ = cµ*c0/2 (Gl. 2.11)
Die Hypotenuse dieses Dreiecks stellt den Anstieg bzw. das Gefälle des kontinuierlichen Verlaufs bµ(b0) dar. Sie wird hier als Gradient des kontinuierlichen Verlaufs bµ(b0) bezeichnet.
topic   (3) Auflösung der Haupteinheiten
Der kontinuierliche Verlauf bµ(b0) soll als Folge von Codewörtern wiedergegeben werden. Jedes Codewort entspricht genau einem Schritt nichtkonstanter Länge in Richtung des Vektors vu0. Das Codewort besteht aus 2 Teilen, einem Vorzeichencode und einem Schrittcode. Die Zahlendarstellung und deren Anordnung innerhalb des Codewortes wird durch diese Verfahrensbeschreibung nicht vorgeben.
Der Zahlenvorrat kann für jede Dimension µ gesondert festgelegt werden. Die Länge des Codewortes xµ der Codefolge der µ-ten Dimension wird hier für die duale Zahlendarstellung definiert. Alle anderen Zahlendarstellungen können darauf zurückgeführt werden. Unter Berücksichtigung einer Stelle für das Vorzeichen
xvµ = 1 (Gl. 3.1)
bleiben
xwµ = xµ - xvµ = xµ - 1 (Gl. 3.2)
Stellen für die Darstellung des Schrittcodes. Insgesamt können
yµ = 2xwµ = 2(xµ - 1) (Gl. 3.3)
unterschiedliche Schrittcodes dargestellt werden. yµ ist also der Zahlenvorrat des Schrittcodes. Der technische Aufwand, aber auch die erreichbare Genauigkeit der Kodierung werden primär von der Darstellungsbreite xµ des Codes und dem Zahlenvorrat yµ festgelegt.
Der Vorzeichencode zvµ hat zur Vereinfachung dieser Verfahrensbeschreibung den Zahlenvorrat -1 und 1:
zvµ = -1, für fallende Gradienten (Gl. 3.4)
zvµ = 1, für steigende Gradienten (Gl. 3.5)
Der Schrittcode zwµ hat den natürlichen Zahlenvorrat:
zwµ = (0, 1, ..., (yµ - 1)) (Gl. 3.6)
Die Hauteinheiten u0, u1, ..., uµ, ..., um werden in jeweils zugeordnete Untereinheiten su0, su1, ..., suµ, ..., sum aufgelöst. Die Auflösung der Untereinheiten suµ und su0 wird nachfolgend beispielhaft für die Haupteinheiten uµ und u0 beschrieben:
Die genannte Auflösung richtet sich für elektronische Lösungen vorzugsweise nach der in den Gl.n 3.2 und 3.3 definierten Codebreite xµ und dem Zahlenvorrat yµ. Der Wert
zµ = yµ - 1 (Gl. 3.7)
wird als gemeinsamer Teiler der Hauteinheiten uµ und u0 in Untereinheiten verwendet. Es wird ein gemeinsamer Teiler für beide Dimensionen verwendet, weil der Winkel des Gradienten in Bezug zur u0-Achse unabhängig von der Codebreite xµ bleiben soll.
uµ = zµ*suµ (Gl. 3.8)
u0 = zµ*su0 (Gl. 3.9)
Die von den Untereinheiten suµ und su0 aufgespannte Einheitsfläche asuµ ist unter Beachtung von Gl.n 2.3, 3.8 und 3.9
asuµ = suµ*su0 = zµ-2*uµ*u0 = zµ-2*auµ (Gl. 3.10).
Die kontinuierlichen Katheten cµ und c0 nach Gl.n 2.9 und 2.10 mit den Haupteinheiten uµ und u0 werden quasi auf diskrete Katheten dµ und d0 mit Untereinheiten suµ und su0 abgebildet. Nach Gl. 3.7 gilt für die Diskretisierung der Katheten:
dµ = zµ*cµ (Gl. 3.11)
d0 = zµ*c0 (Gl. 3.12)
Die maximale Länge der diskreten Katheten dµ und d0 wird praktisch vom Zahlenvorrat yµ bzw. dem gemeinsamen Teiler zµ vorgeben. Sie beträgt für die diskrete Kathete
d0 = zµ (Gl. 3.13).
Die diskrete Dreiecksfläche ist vergleichbar mit Gl. 2.11 und unter Berücksichtigung der Gl. 3.10:
adµ = dµ*d0/2 = zµ2*acµ = zµ2*cµ*c0/2 (Gl. 3.14)
Die diskrete Fläche adµ erfordert eine digitale Verarbeitung. Demgegenüber erfordert die kontinuierliche Fläche acµ eine analoge Verarbeitung.
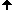topic   (4) Codierung
Während der Codierung wird der Gradienten des kontinuierlichen Verlaufs bµ(b0) in Bezug zur vu0-Richtung beobachtet. Es wird davon ausgegangen, das ein Verlauf mit einem hohen Gradienten viele Informationen enthält und im Vergleich dazu ein Verlauf mit einem flachen Gradienten weniger. Dies gilt sowohl für Anstiege als auch Gefälle im kontinuierlichen Verlauf bµ(b0). Die Informationsdichte und die Dichte der erzeugten Codes haben eine Entsprechung: Hohe Gradienten führen zu vielen Codewörtern, niedrige Gradienten dagegen zu wenigen Codewörtern. Erreicht wird diese schrittweitenabhängige Codierung, indem die kontinuierliche Dreiecksfläche acµ unter dem Gradienten konstant gehalten wird. Die zugehörige diskrete Dreiecksfläche adµ bleibt auch konstant. Sind der Gradient des kontinuierlichen Verlaufs bµ(b0) und die Dreiecksfläche bekannt, liegen die diskreten Katheten dµ und d0 fest und können ausgewertet werden.
Die Größe der konstanten Dreiecksfläche adµC wird von der kleinsten Kathete dµ = 1 suµ und der größten Kathete d0 = zµ gemäß Gl. 3.13 festgelegt:
adµC = dµ*d0/2 = zµ/2 = konst. (Gl. 4.1)
Die konstante Dreiecksfläche acµC, die aus den kontinuierlichen Katheten cµ und c0 besteht, wird aus Gl. 4.1 mit Hilfe von Gl. 3.14 skaliert:
acµC = adµC/zµ2 = 2/zµ = konst. (Gl. 4.2)
Um nichtcodierbare Anteile im kontinuierlichen Verlaufs bµ(b0) auszuschließen und den Gradienten zu gewinnen, wird die kontinuierliche Fläche acµ unter dem kontinuierlichen Verlauf bµ(b0) mit Hilfe eines geeignetes Integrationsverfahren ermittelt. Sie wird während der Integration mit der konstanten Fläche acµC verglichen.
Das Codewort der Codefolge der µ-ten Dimension besteht aus dem Vorzeichencode zvµ und dem Schrittcode zwµ. Der Vorzeichencode zvµ kann definitionsgemäß nach Gl.n 3.4 und 3.5 hier nur die Werte -1 und 1 annehmen:
zvµ = -1, für fallende Gradienten (Gl. 4.3)
zvµ = 1, für steigende Gradienten (Gl. 4.4)
Der Schrittcode zwµ hat einen Zahlenvorrat nach Gl. 3.6 und wird aus der diskreten Kathete d0 unter Weglassung der Untereinheit su0 gebildet:
zwµ = d0/su0 (Gl. 4.5)
Zur Veranschaulichung soll beispielhaft die Zahlendarstellungen des 4-Bit Codes an zwei charakteristischen Gradienten gewonnen werden:
xµ = 4 (Gl. 4.6)
in die Gl.n 3.2 bis 3.4 eingesetzt ergibt:
xwµ = 3 (Gl. 4.7)
yµ = 23 = 8 (Gl. 4.8)
zµ = 7 (Gl. 4.9)
Die konstanten Dreiecksflächen adµC und acµC sind mit der Codebreite xµ = 3, den Zahlenvorrat yµ = 8 und dem gemeinsamen Teiler zµ = 7 festgelegt: In die Gleichungen Gl.n 4.1 und 4.2 eingesetzt, gilt gleichermaßen sowohl für die Codierung als auch für die Decodierung die Vorgabe
adµC = dµ*d0/2 = 3,5 suµ*su0 (Gl. 4.10)
acµC = cµ*c0/2 = 0,071 uµ*u0 (Gl. 4.11).
In Fig 1 sind zwei Gradienten als Geraden (a) und (b) irgendeines Verlaufes bµ(b0) dargestellt. Weiterhin sind in dieser Abbildung die kontinuierlichen Katheten cµ über c0 bezogen auf die Haupteinheiten uµ und u0 und die zugehörigen diskreten Katheten dµ über d0 bezogen auf die Untereinheiten suµ und su0 eingezeichnet. Gut erkennbar ist die Auflösung der Haupteinheiten uµ und u0 in Untereinheiten suµ und su0 mit jeweils zµ Schritten.
Die Geraden (a) und (b) in Fig. 1 entsprechen unterschiedlichen Gradienten irgendeines Verlaufes bµ(b0), denen jeweils ein 4 Bit-Code zugeordnet wird:
Gerade (a):
Gerade (a) charakterisiert den flachsten Gradienten der kodierbar ist. Die diskreten Katheten sind
d0 = 7 su0 (Gl. 4.12)
dµ = 1 suµ (Gl. 4.13)
Das Codewort lautet:
zvµ = 1 (Gl. 4.14)
zwµ = d0/su0 = 7 (Gl. 4.15)
Das Vorzeichen wird in xvµ mit dem Wert 1 codiert. Er weist auf einen ansteigenden Gradienten hin. Der Schritt wird in zwµ mit dem Wert 7 codiert. Dies ist bei der gegeben Codebreite xµ = 4 der größte codierbare Schritt in Richtung des Vektors vu0.
Gerade (b):
Gerade (b) charakterisiert den steilsten Gradienten der kodierbar ist. Die diskreten Katheten sind
d0 = 1 su0 (Gl. 4.16)
dµ = 7 suµ (Gl. 4.17)
Das Codewort lautet:
zvµ = 1 (Gl. 4.18)
zwµ = d0/su0 = 1 (Gl. 4.19)
Das Vorzeichen wird wieder in xvµ mit dem Wert 1 codiert, um auf den ansteigenden Gradienten hinzuweisen. Der Schritt wird in zwµ auch mit dem Wert 1 codiert. Dies ist der kleinste codierbare Schritt in Richtung des Vektors vu0.
Die charakteristischen Gradienten (a) und (b) in Fig. 1 begrenzen drei dort dargestellten Bereiche. Allgemein für alle Zahlendarstellungen verschiedener Länge xµ, die in diesen Bereichen erzeugt werden, gelten folgende Codierungen:
Bereich I:
Der Bereich I befindet sich zwischen Abszisse und der Geraden (a). Liegt der Gradient in diesem Bereich, wird wie folgt codiert:
d0 = zµ (Gl. 4.20)
dµ = 0 (Gl. 4.21)
Das Codewort lautet:
zvµ = -1 oder 1 (Gl. 4.22)
zwµ = d0 = zµ (Gl. 4.23)
Der Schritt wird in zwµ mit dem Wert zµ codiert. In diesem Bereich wird der Decoder angewiesen, einen großen Schritt in Richtung des Vektors vu0 zu tun ohne den decodierten Verlauf aµ(a0) zu verändern.
Es ist nicht notwendig, einen Wert für das Vorzeichen in xvµ zu kodieren, weil der Gradient Null ist. Der freie Platz in der Codefolge wird anders geartet verwendet: Mit folgender Belegung von zvµ wird der Decoder angewiesen, eine weiter unten beschriebene Dynamisierung anzuwenden.
zvµ = -1, der Decoder verwendet keine Dynamisierung (Gl. 4.24)
zvµ = 1, der Decoder verwendet eine Dynamisierung (Gl. 4.25)
Auf entsprechende Ausführungsformen des Decoders wird weiter unten eingegangen.
Bereich II:
Der Bereich II befindet sich zwischen der Geraden (b) und der Ordinate. Liegt der Gradient in diesem Bereich, wird wie folgt codiert:
d0 = 0 (Gl. 4.26)
dµ = zµ (Gl. 4.27)
Das Codewort lautet:
zvµ = 1 (Gl. 4.28)
zwµ = d0 = 0 (Gl. 4.29)
Der Schritt wird in zwµ mit dem Wert 0 codiert. In diesem Bereich wird der Decoder angewiesen, den decodierte Verlauf aµ(a0) nachzuführen ohne einen Schritt in Richtung des Vektors vu0 zu tun.
Bereich III:
Der Bereich III befindet sich zwischen den beiden Geraden (a) und (b). Liegt der Gradient in diesem Bereich, wird das Codewort aus
zvµ = 1 (Gl. 4.30)
zwµ = d0/su0 (Gl. 4.31)
gebildet. In zwµ wird der Wert der diskreten Kathete d0 ohne Einheit festgehalten, der gerade bei dem Ereignis
acµ > acµC bzw. (Gl. 4.32)
acµ > 2/zµ (Gl. 4.33)
ausgezählt wurde.
Die kontinuierliche Dreiecksfläche acµ ergibt sich aus dem Integral von cµ nach b0
b0
ó ó
acµ = ô cµ db0 = ô (bµ - aµ) db0 (Gl. 4.34)
õ õ
(c0) a0
Während der Integration bleibt die obere Grenze des Integrals b0 variabel.
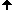topic   (5) Decodierung
Die Decodierung einer Codefolge wird beispielhaft am Verlauf bµ(b0) einer Kosinus-Funktion gemäß Fig. 2 erklärt. Er folgt der analytischen Beschreibung:
bµ(b0) = sqrt(2)*sin(b0) (Gl. 5.1)
Als Amplitude wird der Wert sqrt(2) = 1,414 vorgeben.
Die Gewinnung des 4-Bit-Codes wurde oben ausführlich erläutert. Die Folge des 4-Bit-Codes, die sich aus dem Verlauf in Fig. 2 ergibt, wird in Fig. 3 dargestellt.
Die Codefolge besteht aus 17 Codewörtern. Jedes Codewort besteht aus einem Vorzeichenbit zvµ und einem 3 Bit langen Schrittcode zwµ. Insgesamt werden
17*4 Bit = 68 Bit = 8,5 Byte (Gl. 5.2)
zur Codierung des Verlaufes benötigt.
Der decodierte Verlauf wird in den meisten Anwendung für eine Weiterverarbeitung durch Mikrocontroller, Digitale Signalprozessoren sowie spezielle Mikroprozessoren benötigt. Sie verarbeiten den decodierten Verlauf als ausgewählte Punktefolge:
aµ(a0) = A1(aµ, a0), A2(aµ, a0), ... , An(aµ, a0), ... , AdCounter (aµ, a0) (Gl. 5.3)
Jeder Gradient wird durch ein Geradenstück, dass durch einen Anfangspunkt An - 1(aµ, a0) und eine Endpunkt An(aµ, a0) bestimmt ist, festgelegt. Der Endpunkt An(aµ, a0) ist gleichzeitig der Anfangspunkt für das nachfolgende Geradenstück. Zwischen den Punkten ist der decodierte Verlauf aµ(a0) linear. Jedes Codewort kann vorteilhaft für sich decodiert werden. Insgesamt besteht der decodierte Verlauf aµ(a0) aus einer Anzahl von dCounter Geradenstücken. Er ist kontinuierlich, aber nur stückweise stetig differenzierbar. Diese Darstellungsform eignet sich sehr gut zur vektororientierten grafischen Ausgabe auf einem Display.
Bevor die in Gl. 5.3 beschriebene Punktefolge entsteht, wird während der Decodierung ein weiteres rechtwinkliges Dreieck bestehend aus den decodierten Katheten eµ und e0 gewonnen:
Die Fläche dieses Dreiecks aeµ wird für die Decodierung der konstanten Fläche acµC nach Gl. 4.2 gleichgesetzt:
aeµ = eµ*e0/2 = acµC (Gl. 5.4)
Die erste Kathete e0 entspricht exakt dem mit dem gemeinsamen Teiler zµ (siehe Gl. 3.7) skalierten Schrittcode zwµ
e0 = zwµ/zµ (Gl. 5.5)
Die zweite Kathete eµ ergibt sich aus den Gl.n 5.4 und 5.5 mit
eµ = 2*acµC/e0 = 2*acµC*zµ/zwµ (Gl. 5.6).
Sie wird aus dem Quotienten der Ausdrücke 2*acµC*zµ und zwµ gebildet. Die Art und Weise der Decodierung wird aus diesem Grund Q-Ausführung genannt.
Die decodierte Punktefolge An(aµ, a0) nach Gl. 5.3 entsteht nunmehr, durch die vorzeichenrichtige Summation der decodierten Katheten eµ und e0
aµ := aµ + zvµ*eµ = aµ + 2*zvµ*acµC*zµ/zwµ (Gl. 5.7)
a0 := a0 + e0 = a0 + zwµ/zµ (Gl. 5.8)
Fig 4 zeigt den decodierten Verlauf aµ(a0), der aus der Codefolge in Fig 3 gebildet wurde.
Der Verlauf entspricht der voreingestellten Codebreite xµ = 4 Bit und der Q-Ausführung des Decoders. Er wird in der weiteren Verfahrensbeschreibung noch verbessert.
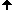top    (6) Anwendungen
Um die kontinuierlichen Katheten cµ und c0 während der Codierung nach den Gl.n 2.9 und 2.10 zu bestimmen, wird der decodierte Verlauf aµ(a0) benötigt. Jeder Codierer besitzt also einen Decodierer, über den die ausgewählte Punktefolge An(aµ, a0) nach Gl. 5.3 in den Codierer zurückgekoppelt wird.
Um Aussagen zur Abbildungsgenauigkeit zu gewinnen, wurde die Eignung des beschriebenen Verfahrens in verschiedenen Ausführungsformen untersucht:
Wird die genannte Rückkopplung modifiziert, indem anstelle von Gl. 5.6 eine einfache Subtraktion des Wertes des Schrittcodes zwµ vom gemeinsamen Teiler zµ
eµ = (zµ - zwµ)/zµ = 1 - zwµ/zµ (Gl. 6.1)
verwendet wird, entstehen zwar modifizierte Codes, aber an der Abbildungsgenauigkeit werden keine Abstriche gemacht. Im Gegensatz zur oben beschriebenen Q-Ausführung, wird die Art und Weise der Decodierung nach Gl. 6.1 S-Ausführung genannt. Die S-Ausführung hat den Vorteil, dass sich der Decoder weitgehend vereinfacht: In allen drei in Fig. 1 definierten Bereichen gelten für die Decodierung in der S-Ausführung die gleichen Verfahrensschritte. Die Codewörter müssen nicht während der Decodierung in Abhängigkeit von der Zugehörigkeit zu den genannten Bereichen vorsortiert werden.
Die Untersuchungen haben gezeigt, dass durch die Anwendung der S-Ausführung keine systematischen Fehler bei der Codierung und Decodierung durch den sogenannten S-Code entstehen. Allerdings sei besonders darauf hingewiesen, dass der S-Code nicht als Q-Code oder umgekehrt decodiert werden darf. Codes beider Ausführungen dürfen nicht vertauscht werden.
Die beschriebene Codierung und Decodierung kann in verschiedenen Ausführungsformen angewendet werden. Die verschiedenen Ausführungsformen unterscheiden sich im Wesentlichen durch die technischen Aufwendungen für den Decoder.
In der Verifizierungsphase des Verfahrens, in der die Eignung für deterministische und stochastische Signale mit Erfolg untersucht wurde, zeigte sich, dass das Verfahren in den Bereichen I und II nach Fig 1 weiter verbessert werden kann. In diesen Bereichen wird dem Decoder nur signalisiert, ob (im Bereich I) der größte Schritt ohne Änderung im decodierten Verlauf aµ(a0) oder (im Bereich II) der kleinste Schritt mit maximaler Änderung im decodierten Verlauf aµ(a0) ausgeführt wird.
In zwei weiteren Ausführungsformen, die dQ- und dS-Ausführung genannt werden, wird in den Bereichen I und II eine Dynamisierung durchgeführt:
Die Ausführungsformen dQ und dS vergrößern im Bereich I automatisch die Länge der decodierten Kathete e0 um den Faktor 2, wenn mehrere Codes aus dem Bereich I hintereinander ausgegeben werden. Der Decoder erkennt, wenn die Codes nach den Gl.n 4.20 bis 4.23 gebildet werden, ob eine Dynamisierung vorgenommen wurde.
Die automatische Dynamisierung im Bereich I kann von außen ein- oder ausgeschaltet werden. Dazu werden dem Speicherplatz qAµ folgende Werte zugewiesen
qA1 = 0, ohne Dynamisierung im Bereich I (Gl. 6.2)
qA1 = 1, mit Dynamisierung im Bereich I (Gl. 6.3),
die ohne Verzögerung an das Vorzeichenbit gemäß Gl.n 4.24 und 4.25 übergeben werden.
Im Gegensatz dazu kann die Dynamisierung im Bereich II nicht von außen ein- oder ausgeschaltet werden:
Die decodierte Kathete eµ, die entweder nach Gl. 5.6 (dQ-Code) oder Gl. 6.1 (dS-Code) gebildet wird, wird jeweils um den Faktor 2 vergrößert. Die Dynamisierung wird, nur dann verwendet, wenn der dQ-Code oder der dS-Code erzeugt wird und mehrere Codes aus dem Bereich II hintereinander ausgegeben werden.
Die Anwendung der automatischen Dynamisierung ermöglicht eine Vorgabe für den ersten Wert der decodierten Kathete eµ im Bereich II. Er wird jeweils zu Beginn der Dynamisierung der decodierten Kathete eµ zugewiesen. Dieser Wert kann von außen vorgeben und im Speicherplatz für Codierer und Decodierer
qA2 = 0,25 (Gl. 6.4),
bereitgehalten werden. Untersuchungen an typischen Verläufen haben gezeigt, dass mit der Einstellung gemäß Gl. 6.4 der decodierte Verlauf aµ(a0) verbessert werden kann. Die Verbesserung wird in Fig. 5 verdeutlicht. Dort wurde für die Codierung und Decodierung der Kosinus-Funktion gemäß Fig. 2 der dQ-Code verwendet.
Der decodierte Verlauf in Fig. 5 wird durch 17 nichtäquidistante Punkte beschrieben. Die Schwingneigung, die durch den Q-Code im decodierten Verlauf aµ(a0) entstanden ist, wurde beim dQ-Code vermieden.
Während Schwingungen gewöhnlich zweidimensional in der Form bµ(b0) dargestellt werden, haben Wellen einen mehrdimensionalen Charakter. Gelingt es, den Verlauf von Wellen, in den eingangs beschriebenen (m + 1)-dimensionalen Funktionsraum zu beschreiben, kann eine mehrdimensionale Codierung und Decodierung mit dem hier beschriebenen Verfahren durchgeführt werden. Er wird prinzipiell zwischen einer seriellen und einer parallelen Verarbeitung unterschieden:
Die parallele Verarbeitung setzt voraus, dass für die Codierung und Decodierung von m Dimensionen (siehe Gl. 2.1) auch m Codierer nebeneinander verwendet werden. Der Datenstrom vom m Codefolgen wird (quasi-) nebeneinander zu m Decodern geführt. Die parallele Verarbeitung wird vorzugsweise zum Codieren und Decodieren von online erzeugten zeitlichen oder räumlichen Verläufen verwendet.
Die serielle Verarbeitung ist vorzugsweise anwendbar wenn die genannten Verläufe über m Dimensionen "off line" vorliegen. Er reicht aus, wenn nur ein Codierer verwendet wird. Die einzelnen Dimensionen können nacheinander codiert bzw. decodiert werden. Der Datenstrom vom m Codefolgen wird abschnittsweise nacheinander geführt. Der Decoder wird dazu zu Beginn eines jeden Abschnittes neu initialisiert. Die Initialisierung wird ausgelöst, indem der Codierer ein Reset-Signal
bReset = true (Gl. 6.5)
erhält. Zusätzlich zur Codefolge werden auch Initialisierungsdaten, insbesondere die Nummer der aktuellen Dimension µ, an den Decoder übergeben.
Auch eine gemischte serielle und parallele Verarbeitung ist denkbar. Sie soll aber an dieser Stelle nicht weiter betrachtet werden.
Die Weiterverarbeitung der mehrdimensionalen Codefolgen nach der Decodierung erfordert ein Verfahren, dass die bezüglich der 0-ten Dimension freilaufenden Codewörter wieder synchronisiert. Dabei werden ausschließlich die für die Weiterverarbeitung notwendigen Dimensionen herangezogen, und der kleinste gemeinsame Abschnitt als MicroStep des Decoders hd durch eine Fensterung der decodierten Katheten e0 der einzelnen Dimensionen gewonnen. Der nebenläufige Charakter der Codefolgen wird dadurch wieder aufgehoben. Die Weiterverarbeitung sollte auch schrittweitengesteuert sein. Ein entsprechendes Verfahren wurde in [JACOB 95.1] vorgestellt.
Das beschriebene Verfahren gewährleistet
- eine hohe Abbildungsgenauigkeit bei vertretbaren Kosten,
- eine störsichere Datenübertragung mit geringem technischen Aufwand,
- eine hohe Übertragungsdichte und geringes Datenvolumen pro Übertragungskanal,
- die gemischte Verarbeitung von on- und off-line-Datenbeständen in Vorhersagemodellen und
- eine große Anwendungsbreite durch universelle Anwendbarkeit.
Der Autor empfiehlt Anwendungen zum Erfassen, Übertragen und Auswerten von Schwingungen und Wellen in den Bereichen Multimedia, Mess-, Diagnose-, Automatisierungstechnik und Strukturanalyse. Das beschriebene Verfahren wird einerseits in Algorithmen überführt (Programmbibliothek), die in Software- oder Firmware-Lösungen u.a. zum Komprimieren von Daten, dem Ermitteln von Kennwerten, der Analyse und audiovisuellen Darstellung verwendet werden. Andererseits wird nach [UML V1.0] aus der Verfahrensbeschreibung direkt das Layout von Hardware-Lösungen (Baugruppen, Schaltkreise, IP-Cores) generiert, die u.a. für die automatische Sprach- und Bildverarbeitung, die Subanalyse [JACOB 95.2] oder Merkmalsbildung [JACOB 97] verwendet werden.
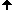top    (7) Literaturverzeichnis

[JACOB 95.1] Christian E. Jacob: Verfahren zur Periodendauer- und Wellenlängenmessung dominanter Schwingungen und Wellen sowie zur Spektralanalyse von Schwingungen und Wellen, OS 195 20 836

[JACOB 95.2] Christian E. Jacob: Analyse von Subspektren mit massiv parallelen Rechnerstrukturen; Vortrag zum 10. ASIM-Workshop "Simulation verteilter Systeme und paralleler Prozesse" der ASIM am FhG-IIS in Dresden 23./24.10.95

[UML 97] Unified Modeling Language (UML) Version 1.0 vom 13.01.1997

[Jacob 97] Christian Jacob: Merkmalsbildung mit den beiden TANDEM-Verfahren, Vortrag im Rahmen der 7. Ebernburger Gespräche der ASIM am 17.04.1997

[Jacob 98] Christian Jacob: Verfahren zum Codieren zeitlicher oder räumlicher Verläufe physikalischer Schwingungen und Wellen in die Zahlendarstellung (Width of Step Coder/Decoder), OS 198 45 813

Christian E. Jacob